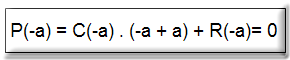Matematica - factoreo de polinomio - operaciones con polinomios

Mostrando las entradas con la etiqueta Factoreo de Polinomios. Mostrar todas las entradas

Estás en: Inicio » Entradas etiquetadas bajo Factoreo de Polinomios

7° Caso: Polinomios de 2° grado y superiores(Parte 2 de 2)

Un método analítico para resolver raíces de un polinomio de grado mayor o igual a 3 puede ser el "Teorema de Gauss" que dice:

Todo número racional de la forma p/q es raíz de un polinomio con coeficientes enteros de forma tal que p es divisor del término independiente y q es divisor del término principal.
Se pueden encontrar todas las raíces de ésta forma o bien luego de encontrar una raíz se divide al polinomio por (x - raíz) usando la regla de Ruffini, de ésta forma vamos disminuyendo el grado del polinomio uno a uno hasta llegar a un polinomio de 2° grado donde aplicamos la fórmula resolvente de las raíces de segundo grado:

7° Caso: Polinomios de 2° grado y superiores(Parte 1 de 2)

Presentación factoreada de un polinomio de 2° grado:

Donde x1 y x2 representan las raíces del polinomio ó bien el punto en donde el polinomio se hace "0".
Éstos valores se obtienen de la aplicación de la siguiente fórmula:

que se obtiene de:

Luego si x1 y x2 son valores para hacer P(x) = 0 entonces:

Aplico un producto a ambos lados de la igualdad para no alterar el resultado:

repito el paso anterior pero ahora con una suma:

de ésta forma creo un trinomio cuadrado perfecto 3° caso de factoreo:

resolviendo:

teniendo en cuenta que una raíz par puede tener 2 resultados:

por último como ésta ecuación posee 2 resultados:

¿Por qué factorear?

¿Para que quiero aprender a factorear?. ¿De qué me sirve?.

En realidad sirve para llegar más rápido y fácil, al resultado de un ejercicio de Cuentas combinadas.

El factorear no es otra cosa que la aplicación de diversos recursos algebraicos.

El factoreo es el primer paso para la resolución de éstas cuentas , luego de factorear se simplifica y por último se procede a resolver.

2° Caso: Factor Común en grupo

El segundo caso se podría decir que es una extensión del 1° caso de factoreo; y tiene la forma de:

5° Caso: Diferencia de Cuadrados

Se factorea como el producto de la suma y diferencia de dos monomios, de la forma:

Puesto que:

4° Caso: Cuatrinomio Cubo Perfecto

El 4° caso es muy parecido al 3° caso de factoreo, se presenta de ésta forma:

Por el 3° caso:

3° Caso: Trinomio Cuadrado Perfecto

Se aplica cuando se tiene un trinomio de grado par, con dos términos que son cuadrados perfectos y un término que es el doble del producto de las bases de los cuadrados perfectos, de ésta manera:

Esto es así por lo siguiente:

Aplico distributiva:

1° Caso: Factor Común

El primer caso es sencillo consiste en extraer el factor común existente en determinada suma, por ejemplo:

Donde "a" es el factor común de ésta suma ya que se repite en ambos términos.
Puesto que:

Es la aplicación de la propiedad distributiva de la multiplicación con respecto a la suma algebraica, sólo que presentada de forma inversa.

Teorema fundamental del álgebra

Un polinomio de grado n positivo tiene exactamente n raíces, considerando las reales y las complejas.

Una consecuencia de este teorema es que un polinomio de grado n tiene como máximo n raíces reales.

En los polinomios a coeficientes reales, las raíces complejas vienen siempre de a pares de allí que un polinomio a coeficientes reales de grado impar siempre tiene por lo menos una raíz real.

Teorema de descomposición factorial de polinomios

Todo polinomio de grado n, positivo, admite una única descomposición en factores de la forma

(x - ai), donde ai es una raíz o cero del polinomio, resultando:

P(x) = an (x - a1). (x - a2)……… (x - an), donde an es el coeficiente principal de P(x) y a1,a2,...,an son n raíces, no necesariamente distintas.

Si al escribir un polinomio como producto hay más de un factor que tiene la misma raíz, a ésta se la llama raíz múltiple, y a la cantidad de veces con que aparece se la llama “grado de multiplicidad”.

Factorización de Polinomios

Recordamos la “descomposición factorial” de un número entero como el producto de potencias de números primos, es decir dado a pertenece a Z, a distinto de 1, a distinto de -1, existen y son únicos los números primos p1, p2,..., pr y los naturales n1, n2, ... , nr tales que:

Esta descomposición factorial de un número entero tiene su análoga para el uso con los polinomios. Diremos que un polinomio de grado positivo ha sido “factoreado” o “factorizado” si ha sido impuesto

en producto de polinomios de grado positivo, primos o no.

Y diremos que ha sido “factoreado total” o “factorizado total” si es primo o si ha sido descompuesto en producto de polinomios primos.

Un polinomio es primo cuando no puede expresarse como un producto de polinomios de menor grado.

Raíces de un Polinomio

Un número a Î R es una raíz o un cero del polinomio

si el valor numérico para x = b es igual a 0.
Es decir, a es raíz de P(x) si

El teorema del resto es una herramienta para reconocer una raíz de un polinomio.

Teorema de “caracterización” de las raíces de un polinomio:

Un número a real es raíz de P(x) sí y solo sí el resto de la división de P(x) por x - a es cero.

Es decir

Demostración: Sabemos que si C(x) es el cociente de la división de P(x) por Q(x), entonces:

pero

reemplazando:

Pero para x = a , se tiene:

Otra forma de enunciar el teorema anterior es: “un número a real es raíz de P(x) sí y sólo sí P(x) es divisible por x - a”.

Es decir:

Nota: el gr (C) = gr (P) – 1

Teorema del Resto

Hipótesis: Sea el polinomio P(x) y otro polinomio Q(x) de la forma Q(x) = (x + a)

Tesis: El resto de la división entre P(x) y Q(x) es igual al valor numérico del polinomio P(x) valorizado en - a es decir P(-a), siendo a un número real.

Demostración: Sabemos que si C(x) es el cociente de la división de P(x) por Q(x), entonces:

, pero

reemplazando:

Pero para x = - a , se tiene:

es decir :

6° Caso: Suma o Diferencia de Potencias de Igual Grado

Son casos en donde hay que realizar una división para conseguir un polinomio mas sencillo de trabajar.
Hay una forma de recordar siempre cómo se resuelven éstos casos que es con una frase, que dice así:

"SeñoR PIPI Nunca Suma Siempre Resta"

La aplicación de estos resultados nos permite factorear binomios que son suma o diferencia de potencias de igual grado.

Descargar ésta entrada: 6° caso.pdf